Find roots, maximum or minimum of quadratic equation
This app is to calculate quadratic equations.
Features
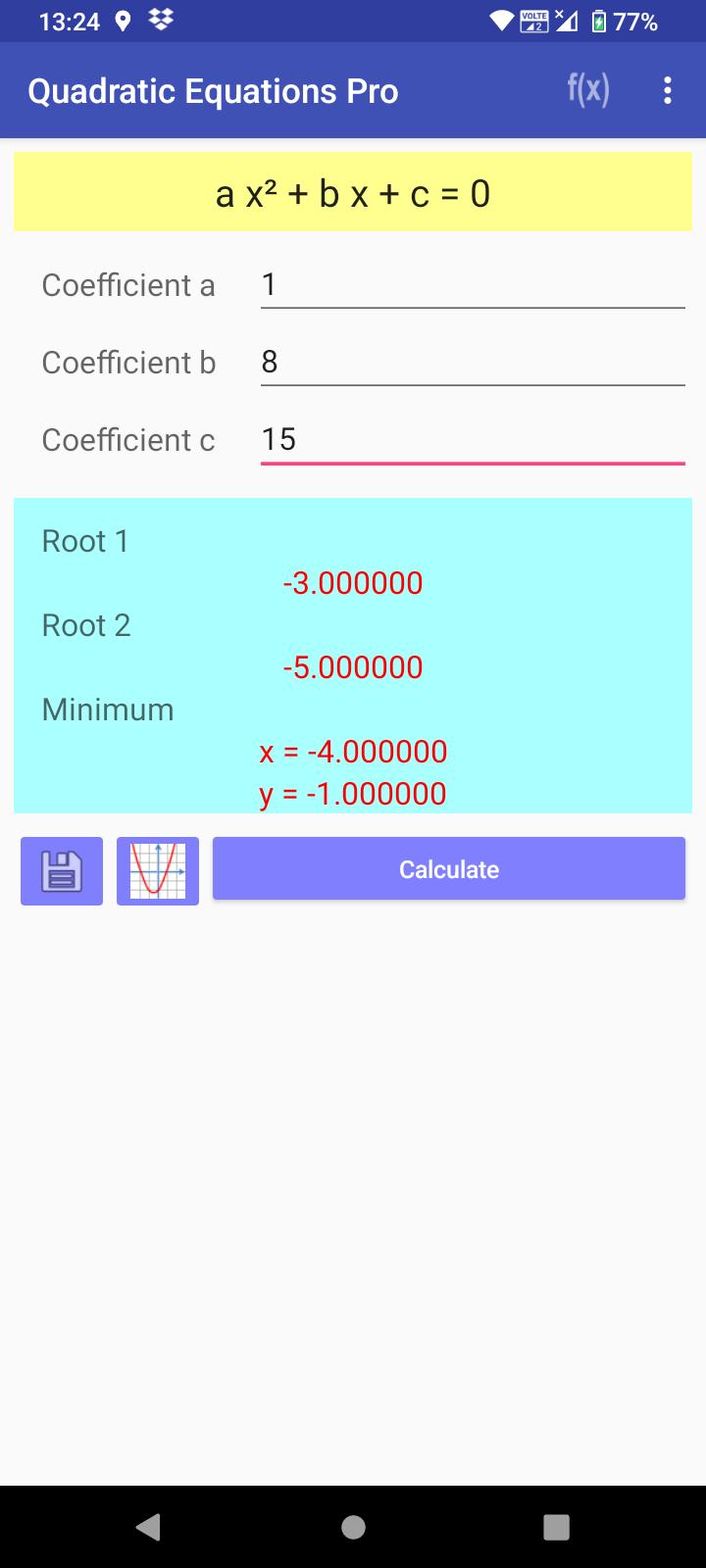
• Solve quadratic equation
• Show real roots and complex roots
• Calculate maximum or minimum point
• Save result in text file
• Support English, German, French, Italian, Spanish, Portuguese, Japanese, Traditional Chinese and Simplified Chinese
Features in PRO version only:
• No Ads
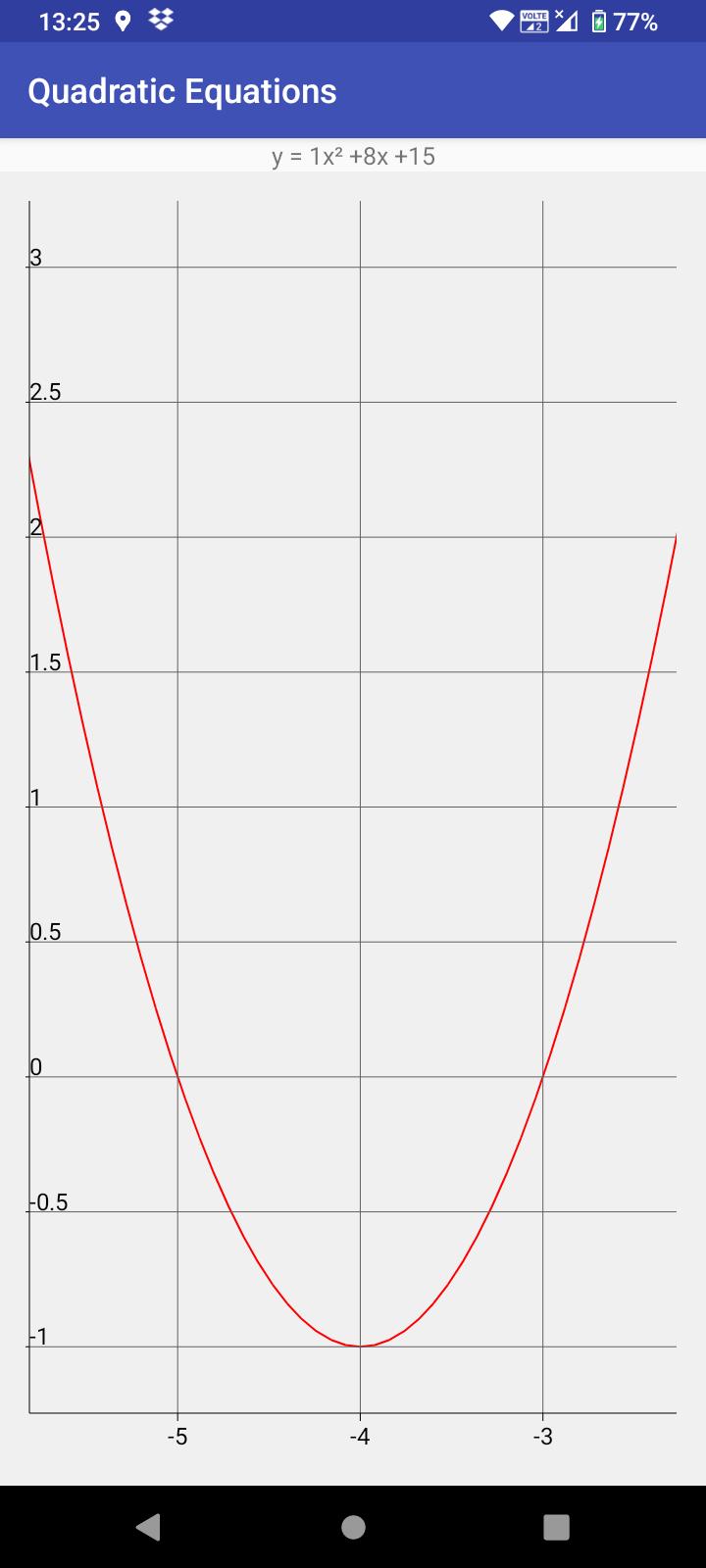
• Show equation in graph
Note :
1. For those who need support please email to me
Do NOT use either the feedback area to write questions, it is not appropriate and that is not guaranteed that can read them.
Quadratic EquationA quadratic equation is an equation of the second degree, meaning it contains a term with the square of a variable. The general form of a quadratic equation is:
```
ax² + bx + c = 0
```
where a, b, and c are constants and a ≠ 0.
Solving Quadratic Equations
There are several methods for solving quadratic equations, including:
1. Factoring:
If the quadratic equation can be factored into two linear factors, it can be solved by setting each factor equal to zero and solving for the variable. For example, if:
```
x² - 5x + 6 = 0
```
can be factored as:
```
(x - 2)(x - 3) = 0
```
then the solutions are x = 2 and x = 3.
2. Completing the Square:
This method involves adding and subtracting a constant to the quadratic equation to create a perfect square trinomial. The square root of the perfect square can then be taken to solve for the variable.
3. Quadratic Formula:
The quadratic formula is a general formula that can be used to solve any quadratic equation:
```
x = (-b ± √(b² - 4ac)) / 2a
```
where a, b, and c are the coefficients of the quadratic equation.
Nature of the Roots
The discriminant of a quadratic equation, which is b² - 4ac, determines the nature of the roots:
* Positive discriminant: Two distinct real roots
* Zero discriminant: One real root (a double root)
* Negative discriminant: No real roots (two complex roots)
Applications of Quadratic Equations
Quadratic equations have numerous applications in various fields, including:
* Projectile motion
* Circuit analysis
* Optimization problems
* Modeling parabolic curves
* Solving geometric problems
Find roots, maximum or minimum of quadratic equation
This app is to calculate quadratic equations.
Features
• Solve quadratic equation
• Show real roots and complex roots
• Calculate maximum or minimum point
• Save result in text file
• Support English, German, French, Italian, Spanish, Portuguese, Japanese, Traditional Chinese and Simplified Chinese
Features in PRO version only:
• No Ads
• Show equation in graph
Note :
1. For those who need support please email to me
Do NOT use either the feedback area to write questions, it is not appropriate and that is not guaranteed that can read them.
Quadratic EquationA quadratic equation is an equation of the second degree, meaning it contains a term with the square of a variable. The general form of a quadratic equation is:
```
ax² + bx + c = 0
```
where a, b, and c are constants and a ≠ 0.
Solving Quadratic Equations
There are several methods for solving quadratic equations, including:
1. Factoring:
If the quadratic equation can be factored into two linear factors, it can be solved by setting each factor equal to zero and solving for the variable. For example, if:
```
x² - 5x + 6 = 0
```
can be factored as:
```
(x - 2)(x - 3) = 0
```
then the solutions are x = 2 and x = 3.
2. Completing the Square:
This method involves adding and subtracting a constant to the quadratic equation to create a perfect square trinomial. The square root of the perfect square can then be taken to solve for the variable.
3. Quadratic Formula:
The quadratic formula is a general formula that can be used to solve any quadratic equation:
```
x = (-b ± √(b² - 4ac)) / 2a
```
where a, b, and c are the coefficients of the quadratic equation.
Nature of the Roots
The discriminant of a quadratic equation, which is b² - 4ac, determines the nature of the roots:
* Positive discriminant: Two distinct real roots
* Zero discriminant: One real root (a double root)
* Negative discriminant: No real roots (two complex roots)
Applications of Quadratic Equations
Quadratic equations have numerous applications in various fields, including:
* Projectile motion
* Circuit analysis
* Optimization problems
* Modeling parabolic curves
* Solving geometric problems