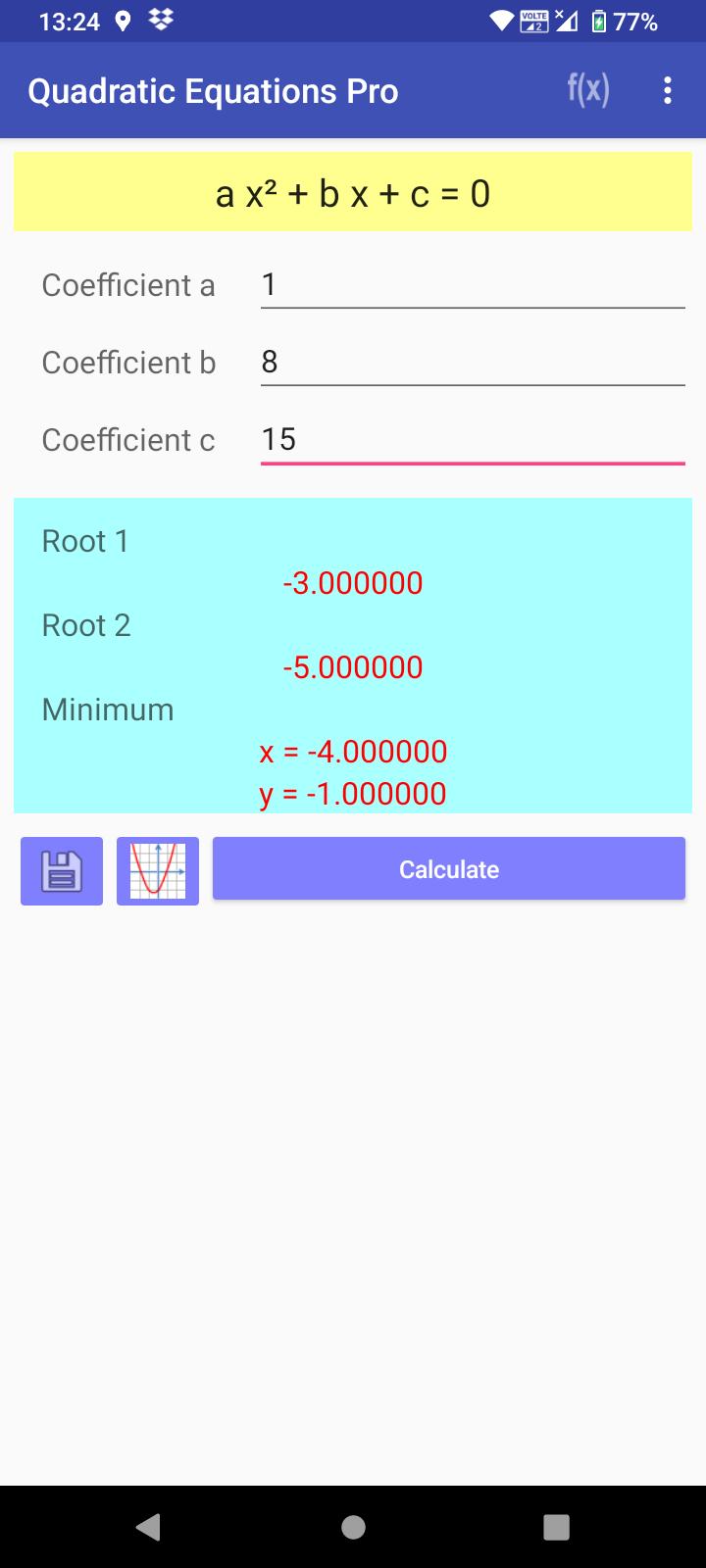
求二次方程式的根、最大值或最小值

該應用程式用於計算二次方程式。

特徵

• 求解二次方程

• 顯示實根和複根

• 計算最大或最小點

• 將結果儲存在文字檔案中

• 支援英語、德語、法語、義大利語、西班牙語、葡萄牙語、日語、繁體中文和簡體中文

僅 PRO 版本的功能：

• 無廣告

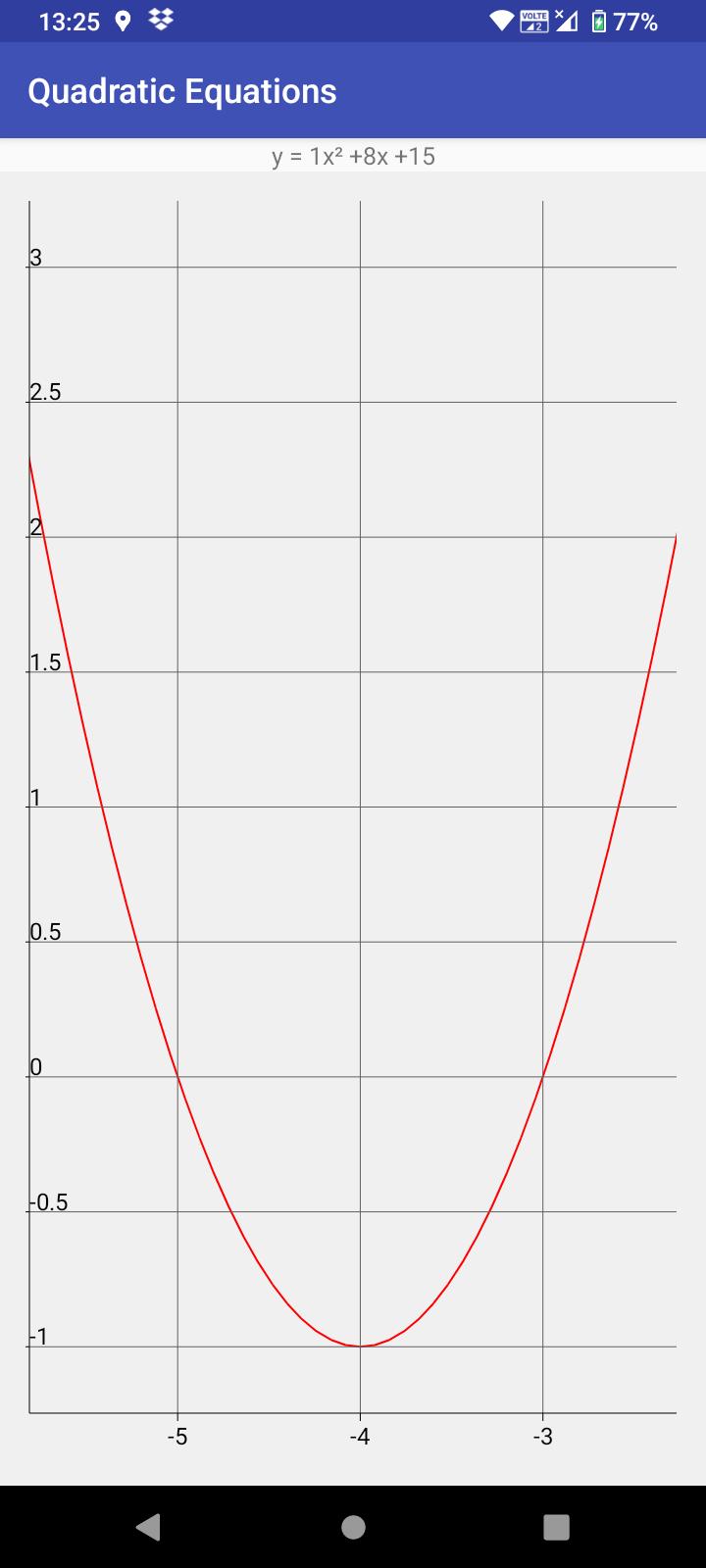
• 在圖表中顯示方程

筆記 ：

1. 對於需要支持的人，請發電子郵件給我

請勿使用回饋區域寫問題，這是不合適的，並且不保證可以閱讀它們。

二次方程是二階方程，這意味著它包含一個變數平方項。二次方程式的一般形式為：

```

ax² + bx + c = 0

```

其中 a、b 和 c 是常數，且 a ≠ 0。

求解二次方程

求解二次方程式的方法有多種，包括：

1. 保理：

如果二次方程式可以分解為兩個線性因子，則可以透過將每個因子設為零並求解變數來求解。例如，如果：

```

x² - 5x + 6 = 0

```

可以分解為：

```

(x - 2)(x - 3) = 0

```

則解為 x = 2 和 x = 3。

2. 完成正方形：

此方法涉及在二次方程中添加和減去一個常數以創建完美的平方三項式。然後可以採用完美平方的平方根來求解變數。

3.二次公式：

二次方程式是一個通用公式，可用來求解任何二次方程式：

```

x = (-b ± √(b² - 4ac)) / 2a

```

其中 a、b 和 c 是二次方程式的係數。

根源的本質

二次方程式的判別式為 b² - 4ac，決定了根的性質：

* 正判別式：兩個不同的實根

* 零判別式：一個實根（雙根）

* 負判別式：無實根（兩個複根）

二次方程式的應用

二次方程式在各領域都有廣泛的應用，包括：

* 拋射運動

* 電路分析

* 最佳化問題

* 拋物線建模

* 解決幾何問題

求二次方程式的根、最大值或最小值

該應用程式用於計算二次方程式。

特徵

• 求解二次方程

• 顯示實根和複根

• 計算最大或最小點

• 將結果儲存在文字檔案中

• 支援英語、德語、法語、義大利語、西班牙語、葡萄牙語、日語、繁體中文和簡體中文

僅 PRO 版本的功能：

• 無廣告

• 在圖表中顯示方程

筆記 ：

1. 對於需要支持的人，請發電子郵件給我

請勿使用回饋區域寫問題，這是不合適的，並且不保證可以閱讀它們。

二次方程是二階方程，這意味著它包含一個變數平方項。二次方程式的一般形式為：

```

ax² + bx + c = 0

```

其中 a、b 和 c 是常數，且 a ≠ 0。

求解二次方程

求解二次方程式的方法有多種，包括：

1. 保理：

如果二次方程式可以分解為兩個線性因子，則可以透過將每個因子設為零並求解變數來求解。例如，如果：

```

x² - 5x + 6 = 0

```

可以分解為：

```

(x - 2)(x - 3) = 0

```

則解為 x = 2 和 x = 3。

2. 完成正方形：

此方法涉及在二次方程中添加和減去一個常數以創建完美的平方三項式。然後可以採用完美平方的平方根來求解變數。

3.二次公式：

二次方程式是一個通用公式，可用來求解任何二次方程式：

```

x = (-b ± √(b² - 4ac)) / 2a

```

其中 a、b 和 c 是二次方程式的係數。

根源的本質

二次方程式的判別式為 b² - 4ac，決定了根的性質：

* 正判別式：兩個不同的實根

* 零判別式：一個實根（雙根）

* 負判別式：無實根（兩個複根）

二次方程式的應用

二次方程式在各領域都有廣泛的應用，包括：

* 拋射運動

* 電路分析

* 最佳化問題

* 拋物線建模

* 解決幾何問題