Encuentra raíces, máximo o mínimo de una ecuación cuadrática
Esta aplicación es para calcular ecuaciones cuadráticas.
Características
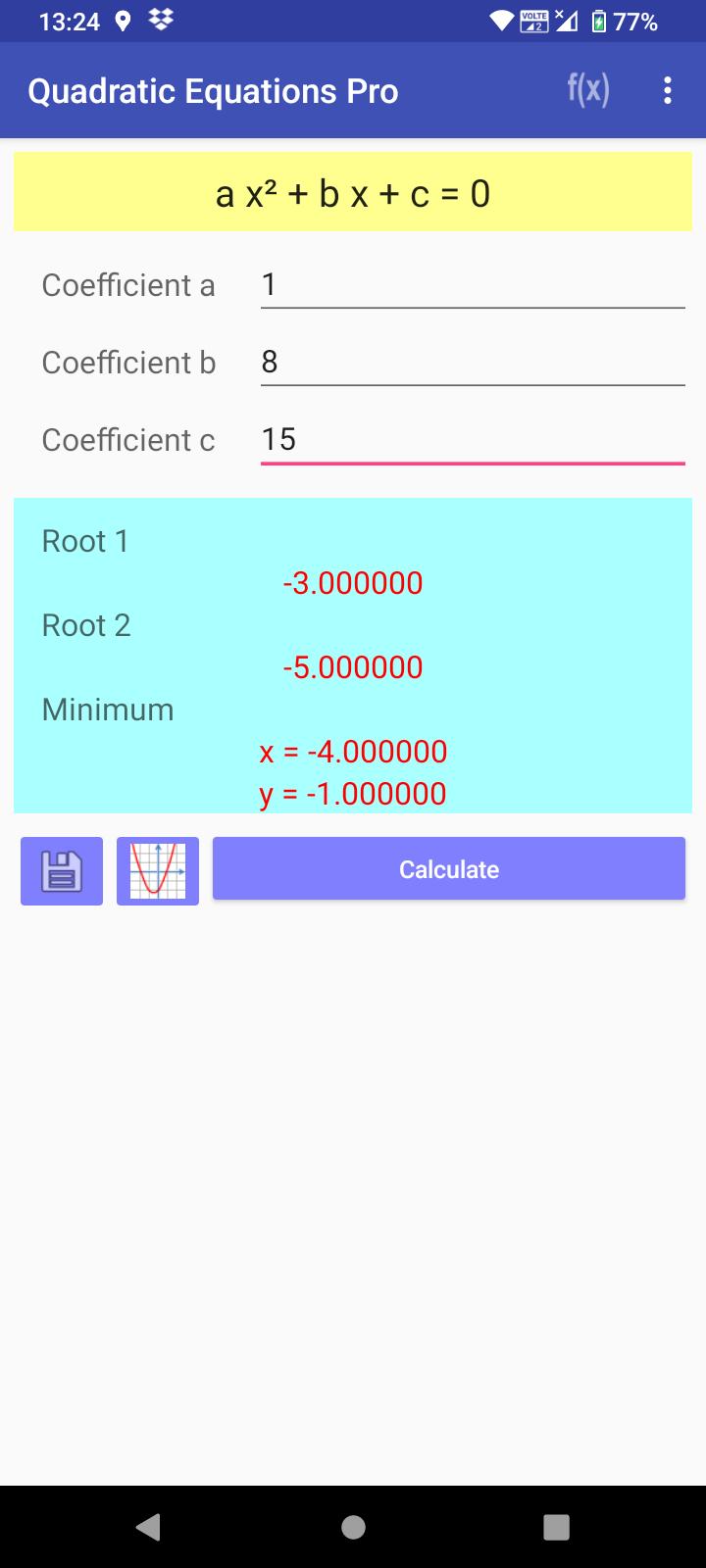
• Resolver ecuación cuadrática
• Mostrar raíces reales y raíces complejas
• Calcular punto máximo o mínimo
• Guardar resultado en archivo de texto
• Compatible con inglés, alemán, francés, italiano, español, portugués, japonés, chino tradicional y chino simplificado
Funciones solo en la versión PRO:
• No Anuncios
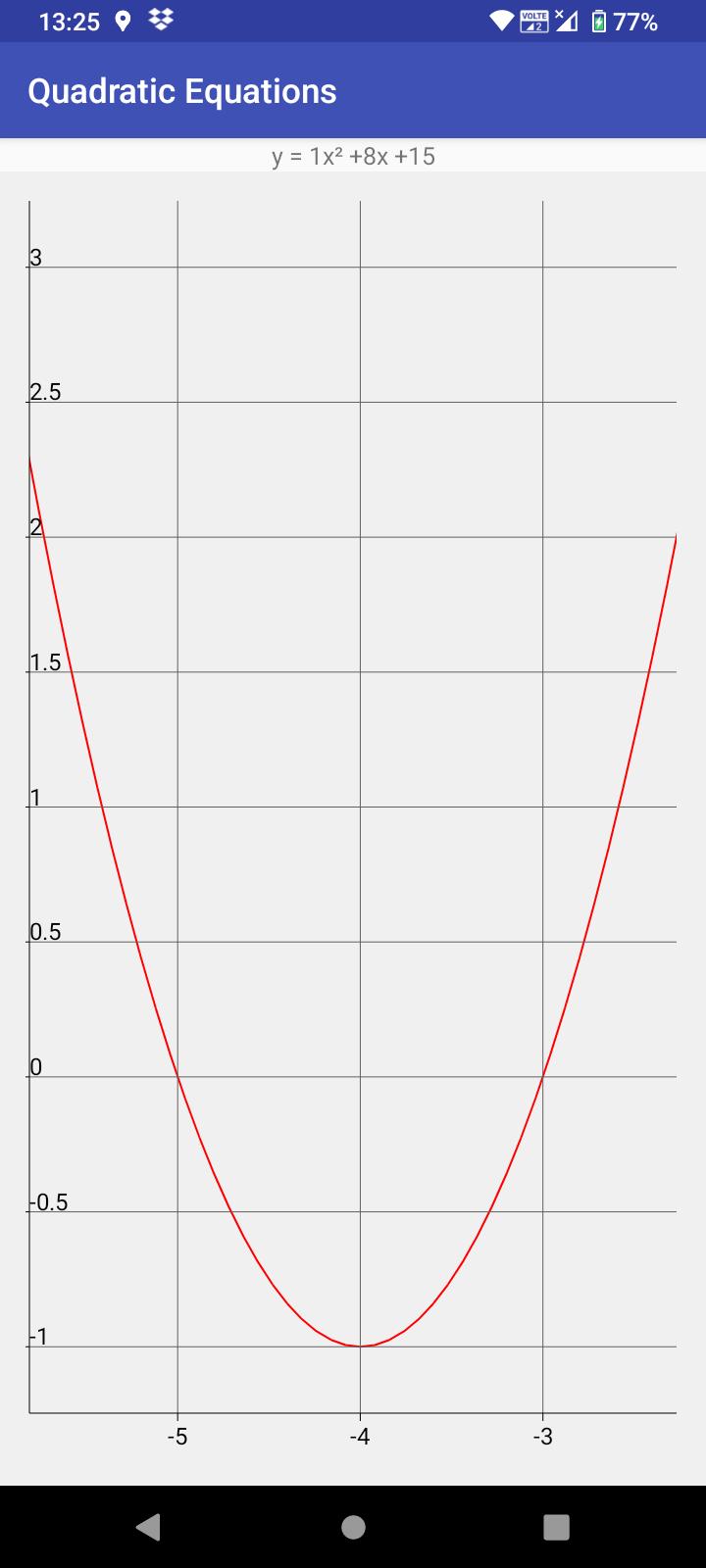
• Mostrar ecuación en gráfico
Nota:
1. Para aquellos que necesitan ayuda, envíenme un correo electrónico.
NO utilice el área de comentarios para escribir preguntas, no es apropiado y no se garantiza que pueda leerlas.
Ecuación cuadráticaUna ecuación cuadrática es una ecuación de segundo grado, lo que significa que contiene un término con el cuadrado de una variable. La forma general de una ecuación cuadrática es:
```
ax² + bx + c = 0
```
donde a, byc son constantes y a ≠ 0.
Resolver ecuaciones cuadráticas
Existen varios métodos para resolver ecuaciones cuadráticas, que incluyen:
1. Factorización:
Si la ecuación cuadrática se puede factorizar en dos factores lineales, se puede resolver igualando cada factor a cero y resolviendo la variable. Por ejemplo, si:
```
x² - 5x + 6 = 0
```
se puede factorizar como:
```
(x - 2)(x - 3) = 0
```
entonces las soluciones son x = 2 y x = 3.
2. Completando el Cuadrado:
Este método implica sumar y restar una constante a la ecuación cuadrática para crear un trinomio cuadrado perfecto. Luego se puede tomar la raíz cuadrada del cuadrado perfecto para resolver la variable.
3. Fórmula cuadrática:
La fórmula cuadrática es una fórmula general que se puede utilizar para resolver cualquier ecuación cuadrática:
```
x = (-b ± √(b² - 4ac)) / 2a
```
donde a, b y c son los coeficientes de la ecuación cuadrática.
Naturaleza de las raíces
El discriminante de una ecuación cuadrática, que es b² - 4ac, determina la naturaleza de las raíces:
* Discriminante positivo: Dos raíces reales distintas
*Cero discriminante: Una raíz real (una raíz doble)
* Discriminante negativo: Sin raíces reales (dos raíces complejas)
Aplicaciones de ecuaciones cuadráticas
Las ecuaciones cuadráticas tienen numerosas aplicaciones en diversos campos, entre ellos:
* Movimiento de proyectil
* Análisis de circuitos
* Problemas de optimización
* Modelado de curvas parabólicas.
*Resolver problemas geométricos
Encuentra raíces, máximo o mínimo de una ecuación cuadrática
Esta aplicación es para calcular ecuaciones cuadráticas.
Características
• Resolver ecuación cuadrática
• Mostrar raíces reales y raíces complejas
• Calcular punto máximo o mínimo
• Guardar resultado en archivo de texto
• Compatible con inglés, alemán, francés, italiano, español, portugués, japonés, chino tradicional y chino simplificado
Funciones solo en la versión PRO:
• No Anuncios
• Mostrar ecuación en gráfico
Nota:
1. Para aquellos que necesitan ayuda, envíenme un correo electrónico.
NO utilice el área de comentarios para escribir preguntas, no es apropiado y no se garantiza que pueda leerlas.
Ecuación cuadráticaUna ecuación cuadrática es una ecuación de segundo grado, lo que significa que contiene un término con el cuadrado de una variable. La forma general de una ecuación cuadrática es:
```
ax² + bx + c = 0
```
donde a, byc son constantes y a ≠ 0.
Resolver ecuaciones cuadráticas
Existen varios métodos para resolver ecuaciones cuadráticas, que incluyen:
1. Factorización:
Si la ecuación cuadrática se puede factorizar en dos factores lineales, se puede resolver igualando cada factor a cero y resolviendo la variable. Por ejemplo, si:
```
x² - 5x + 6 = 0
```
se puede factorizar como:
```
(x - 2)(x - 3) = 0
```
entonces las soluciones son x = 2 y x = 3.
2. Completando el Cuadrado:
Este método implica sumar y restar una constante a la ecuación cuadrática para crear un trinomio cuadrado perfecto. Luego se puede tomar la raíz cuadrada del cuadrado perfecto para resolver la variable.
3. Fórmula cuadrática:
La fórmula cuadrática es una fórmula general que se puede utilizar para resolver cualquier ecuación cuadrática:
```
x = (-b ± √(b² - 4ac)) / 2a
```
donde a, b y c son los coeficientes de la ecuación cuadrática.
Naturaleza de las raíces
El discriminante de una ecuación cuadrática, que es b² - 4ac, determina la naturaleza de las raíces:
* Discriminante positivo: Dos raíces reales distintas
*Cero discriminante: Una raíz real (una raíz doble)
* Discriminante negativo: Sin raíces reales (dos raíces complejas)
Aplicaciones de ecuaciones cuadráticas
Las ecuaciones cuadráticas tienen numerosas aplicaciones en diversos campos, entre ellos:
* Movimiento de proyectil
* Análisis de circuitos
* Problemas de optimización
* Modelado de curvas parabólicas.
*Resolver problemas geométricos