Найти корни, максимум или минимум квадратного уравнения
Это приложение предназначено для расчета квадратных уравнений.
Функции
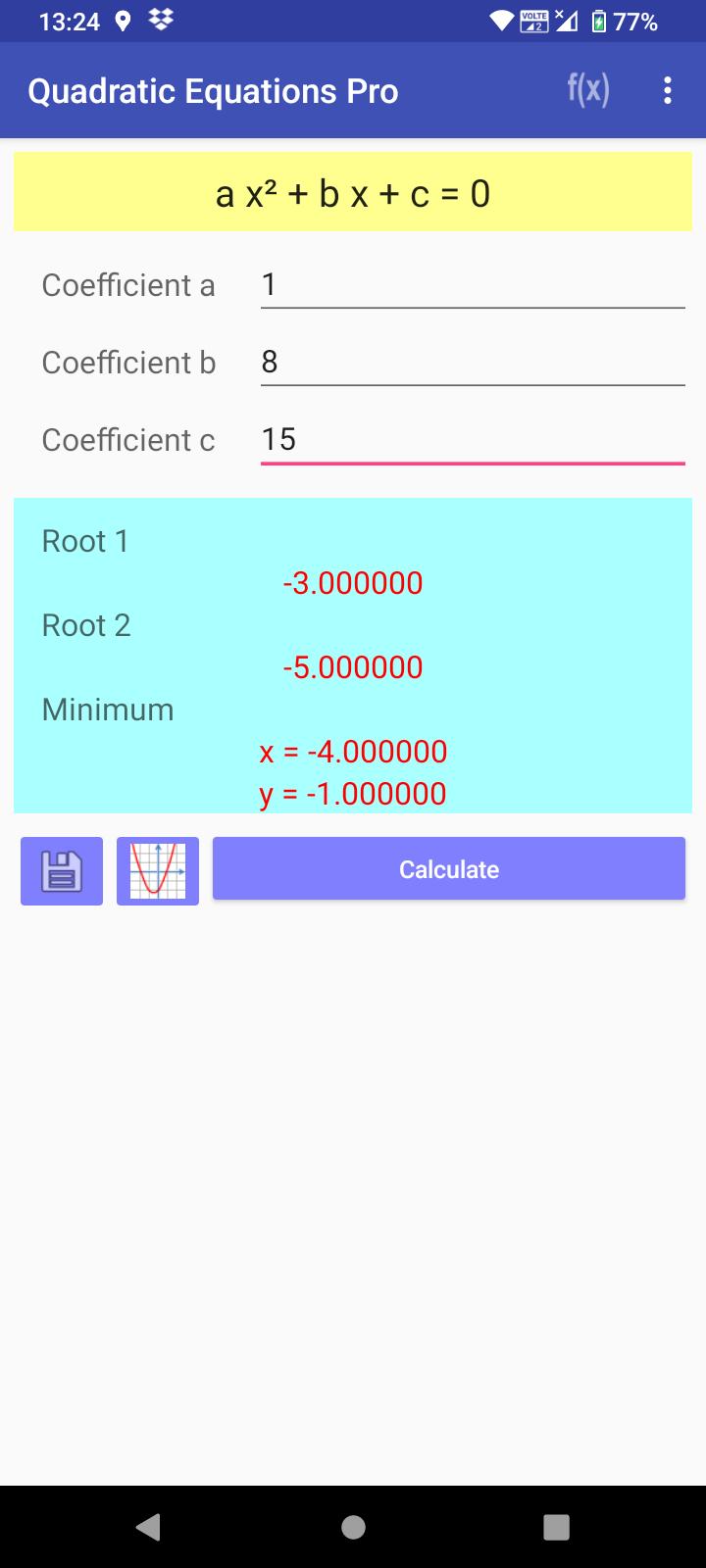
• Решить квадратное уравнение
• Показать действительные и комплексные корни
• Вычислить максимальную или минимальную точку
• Сохранить результат в текстовом файле
• Поддержка английского, немецкого, французского, итальянского, испанского, португальского, японского, традиционного и упрощенного китайского языков. Китайский
Функции только в PRO-версии:
• Без рекламы
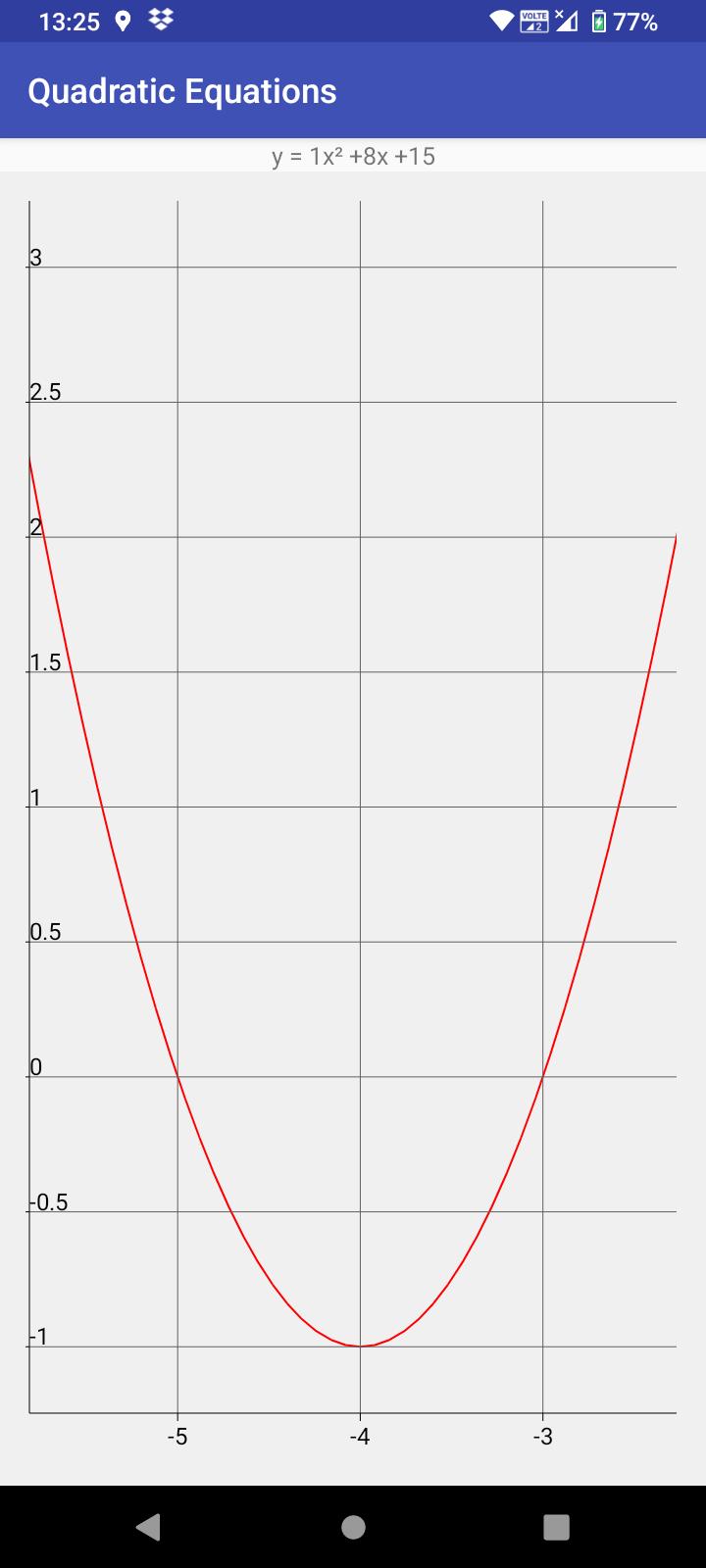
• Показать уравнение на графике
Примечание:
1. Для тех, кто нуждается в поддержке, пожалуйста, напишите мне по электронной почте.
НЕ используйте область обратной связи для написания вопросов, это неуместно и не гарантируется, что вы сможете их прочитать.
Квадратное уравнениеКвадратное уравнение — это уравнение второй степени, то есть оно содержит член с квадратом переменной. Общая форма квадратного уравнения:
```
ах² + bx + c = 0
```
где a, b и c — константы, а a ≠ 0.
Решение квадратных уравнений
Существует несколько методов решения квадратных уравнений, в том числе:
1. Факторинг:
Если квадратное уравнение можно разложить на два линейных фактора, его можно решить, установив каждый фактор равным нулю и определив переменную. Например, если:
```
х² - 5х + 6 = 0
```
можно факторизовать как:
```
(х - 2)(х - 3) = 0
```
тогда решения будут x = 2 и x = 3.
2. Завершение квадрата:
Этот метод включает в себя добавление и вычитание константы из квадратного уравнения для получения идеального квадратного трехчлена. Затем для определения переменной можно использовать квадратный корень из идеального квадрата.
3. Квадратичная формула:
Квадратная формула — это общая формула, которую можно использовать для решения любого квадратного уравнения:
```
х = (-b ± √(b² - 4ac)) / 2a
```
где a, b и c — коэффициенты квадратного уравнения.
Природа корней
Дискриминант квадратного уравнения, который равен b² – 4ac, определяет характер корней:
* Положительный дискриминант: два различных вещественных корня.
* Нулевой дискриминант: один действительный корень (двойной корень).
* Отрицательный дискриминант: действительных корней нет (два комплексных корня).
Приложения квадратных уравнений
Квадратные уравнения имеют множество применений в различных областях, в том числе:
* Движение снаряда
* Анализ схемы
* Проблемы с оптимизацией
* Моделирование параболических кривых
* Решение геометрических задач.
Найти корни, максимум или минимум квадратного уравнения
Это приложение предназначено для расчета квадратных уравнений.
Функции
• Решить квадратное уравнение
• Показать действительные и комплексные корни
• Вычислить максимальную или минимальную точку
• Сохранить результат в текстовом файле
• Поддержка английского, немецкого, французского, итальянского, испанского, португальского, японского, традиционного и упрощенного китайского языков. Китайский
Функции только в PRO-версии:
• Без рекламы
• Показать уравнение на графике
Примечание:
1. Для тех, кто нуждается в поддержке, пожалуйста, напишите мне по электронной почте.
НЕ используйте область обратной связи для написания вопросов, это неуместно и не гарантируется, что вы сможете их прочитать.
Квадратное уравнениеКвадратное уравнение — это уравнение второй степени, то есть оно содержит член с квадратом переменной. Общая форма квадратного уравнения:
```
ах² + bx + c = 0
```
где a, b и c — константы, а a ≠ 0.
Решение квадратных уравнений
Существует несколько методов решения квадратных уравнений, в том числе:
1. Факторинг:
Если квадратное уравнение можно разложить на два линейных фактора, его можно решить, установив каждый фактор равным нулю и определив переменную. Например, если:
```
х² - 5х + 6 = 0
```
можно факторизовать как:
```
(х - 2)(х - 3) = 0
```
тогда решения будут x = 2 и x = 3.
2. Завершение квадрата:
Этот метод включает в себя добавление и вычитание константы из квадратного уравнения для получения идеального квадратного трехчлена. Затем для определения переменной можно использовать квадратный корень из идеального квадрата.
3. Квадратичная формула:
Квадратная формула — это общая формула, которую можно использовать для решения любого квадратного уравнения:
```
х = (-b ± √(b² - 4ac)) / 2a
```
где a, b и c — коэффициенты квадратного уравнения.
Природа корней
Дискриминант квадратного уравнения, который равен b² – 4ac, определяет характер корней:
* Положительный дискриминант: два различных вещественных корня.
* Нулевой дискриминант: один действительный корень (двойной корень).
* Отрицательный дискриминант: действительных корней нет (два комплексных корня).
Приложения квадратных уравнений
Квадратные уравнения имеют множество применений в различных областях, в том числе:
* Движение снаряда
* Анализ схемы
* Проблемы с оптимизацией
* Моделирование параболических кривых
* Решение геометрических задач.