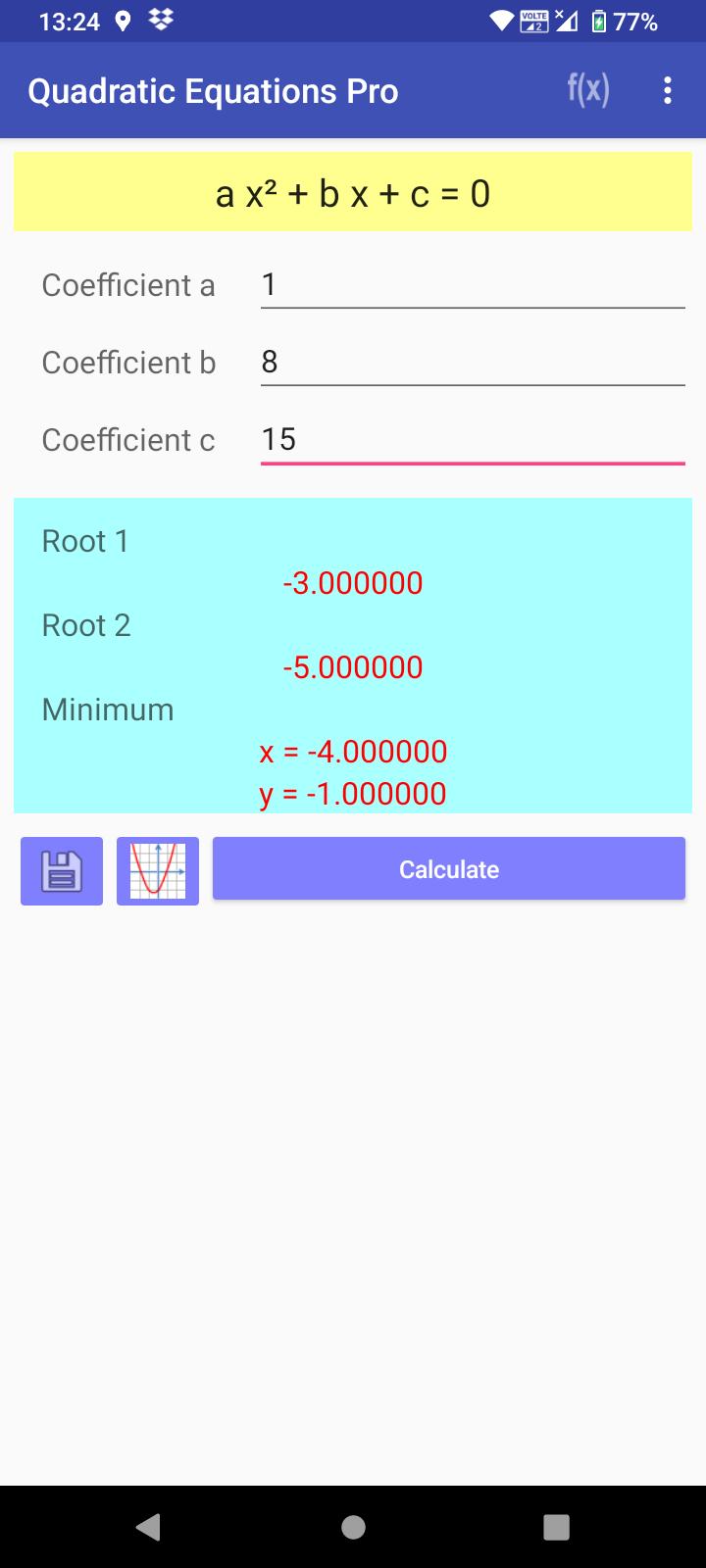
求二次方程的根、最大值或最小值
此应用程序用于计算二次方程。
功能
•求解二次方程
• 显示实根和复根
• 计算最大或最小点
• 将结果保存在文本文件中
• 支持英语、德语、法语、意大利语、西班牙语、葡萄牙语、日语、繁体中文和简体中文
仅限 PRO 版本的功能:
• 无广告
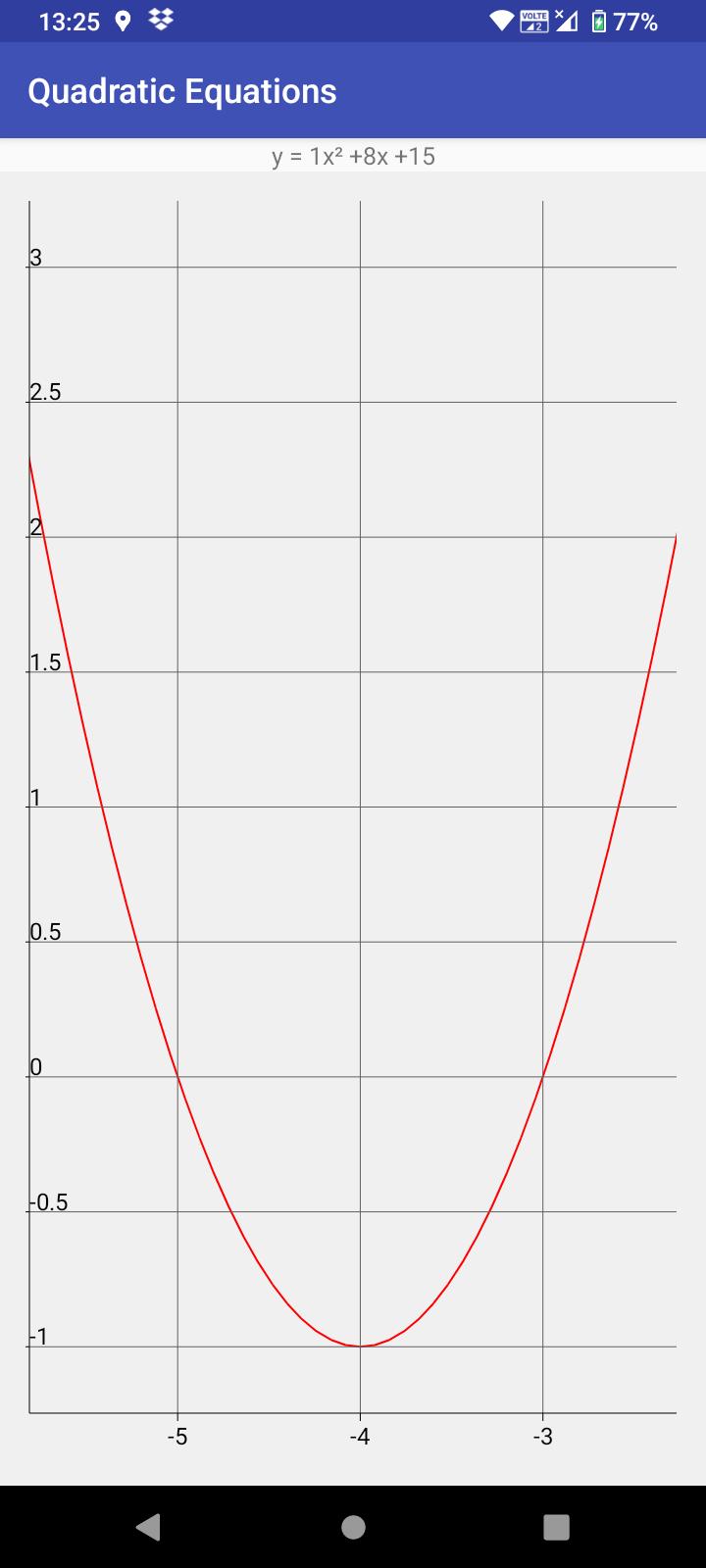
• 在图表中显示方程式< /p>
注意:
1.对于那些需要支持的人,请发送电子邮件给我
不要使用任何反馈区域来写问题,这是不合适的,并且不能保证可以阅读它们。
二次方程二次方程是二阶方程,这意味着它包含一个变量平方项。二次方程的一般形式为:
````
ax² + bx + c = 0
````
其中 a、b 和 c 是常数,且 a ≠ 0。
求解二次方程
求解二次方程的方法有多种,包括:
1. 保理:
如果二次方程可以分解为两个线性因子,则可以通过将每个因子设置为零并求解变量来求解。例如,如果:
````
x² - 5x + 6 = 0
````
可以分解为:
````
(x - 2)(x - 3) = 0
````
则解为 x = 2 和 x = 3。
2. 完成正方形:
此方法涉及在二次方程中添加和减去一个常数以创建完美的平方三项式。然后可以采用完美平方的平方根来求解变量。
3.二次公式:
二次方程是一个通用公式,可用于求解任何二次方程:
````
x = (-b ± √(b² - 4ac)) / 2a
````
其中 a、b 和 c 是二次方程的系数。
根源的本质
二次方程的判别式为 b² - 4ac,决定了根的性质:
* 正判别式:两个不同的实根
* 零判别式:一个实根(双根)
* 负判别式:无实根(两个复根)
二次方程的应用
二次方程在各个领域都有广泛的应用,包括:
* 抛射运动
* 电路分析
* 优化问题
* 抛物线建模
* 解决几何问题
求二次方程的根、最大值或最小值
此应用程序用于计算二次方程。
功能
•求解二次方程
• 显示实根和复根
• 计算最大或最小点
• 将结果保存在文本文件中
• 支持英语、德语、法语、意大利语、西班牙语、葡萄牙语、日语、繁体中文和简体中文
仅限 PRO 版本的功能:
• 无广告
• 在图表中显示方程式< /p>
注意:
1.对于那些需要支持的人,请发送电子邮件给我
不要使用任何反馈区域来写问题,这是不合适的,并且不能保证可以阅读它们。
二次方程二次方程是二阶方程,这意味着它包含一个变量平方项。二次方程的一般形式为:
````
ax² + bx + c = 0
````
其中 a、b 和 c 是常数,且 a ≠ 0。
求解二次方程
求解二次方程的方法有多种,包括:
1. 保理:
如果二次方程可以分解为两个线性因子,则可以通过将每个因子设置为零并求解变量来求解。例如,如果:
````
x² - 5x + 6 = 0
````
可以分解为:
````
(x - 2)(x - 3) = 0
````
则解为 x = 2 和 x = 3。
2. 完成正方形:
此方法涉及在二次方程中添加和减去一个常数以创建完美的平方三项式。然后可以采用完美平方的平方根来求解变量。
3.二次公式:
二次方程是一个通用公式,可用于求解任何二次方程:
````
x = (-b ± √(b² - 4ac)) / 2a
````
其中 a、b 和 c 是二次方程的系数。
根源的本质
二次方程的判别式为 b² - 4ac,决定了根的性质:
* 正判别式:两个不同的实根
* 零判别式:一个实根(双根)
* 负判别式:无实根(两个复根)
二次方程的应用
二次方程在各个领域都有广泛的应用,包括:
* 抛射运动
* 电路分析
* 优化问题
* 抛物线建模
* 解决几何问题