Encontre raízes, máximo ou mínimo da equação quadrática

Este aplicativo serve para calcular equações quadráticas.

Características

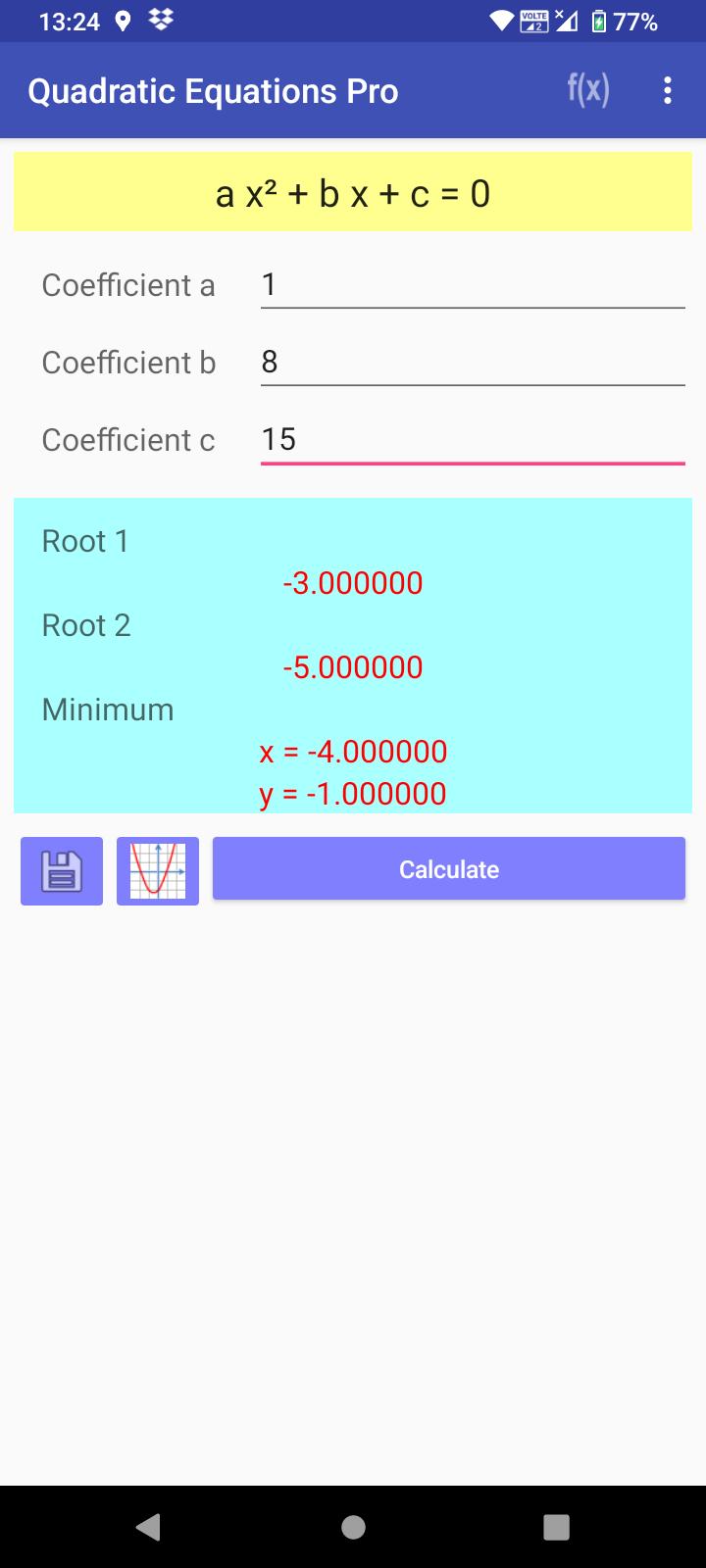
• Resolver equação quadrática

• Mostrar raízes reais e raízes complexas

• Calcular ponto máximo ou mínimo

• Salvar resultado em arquivo de texto

• Suporte em inglês, alemão, francês, italiano, espanhol, português, japonês, chinês tradicional e chinês simplificado

Recursos apenas na versão PRO:

• Sem anúncios

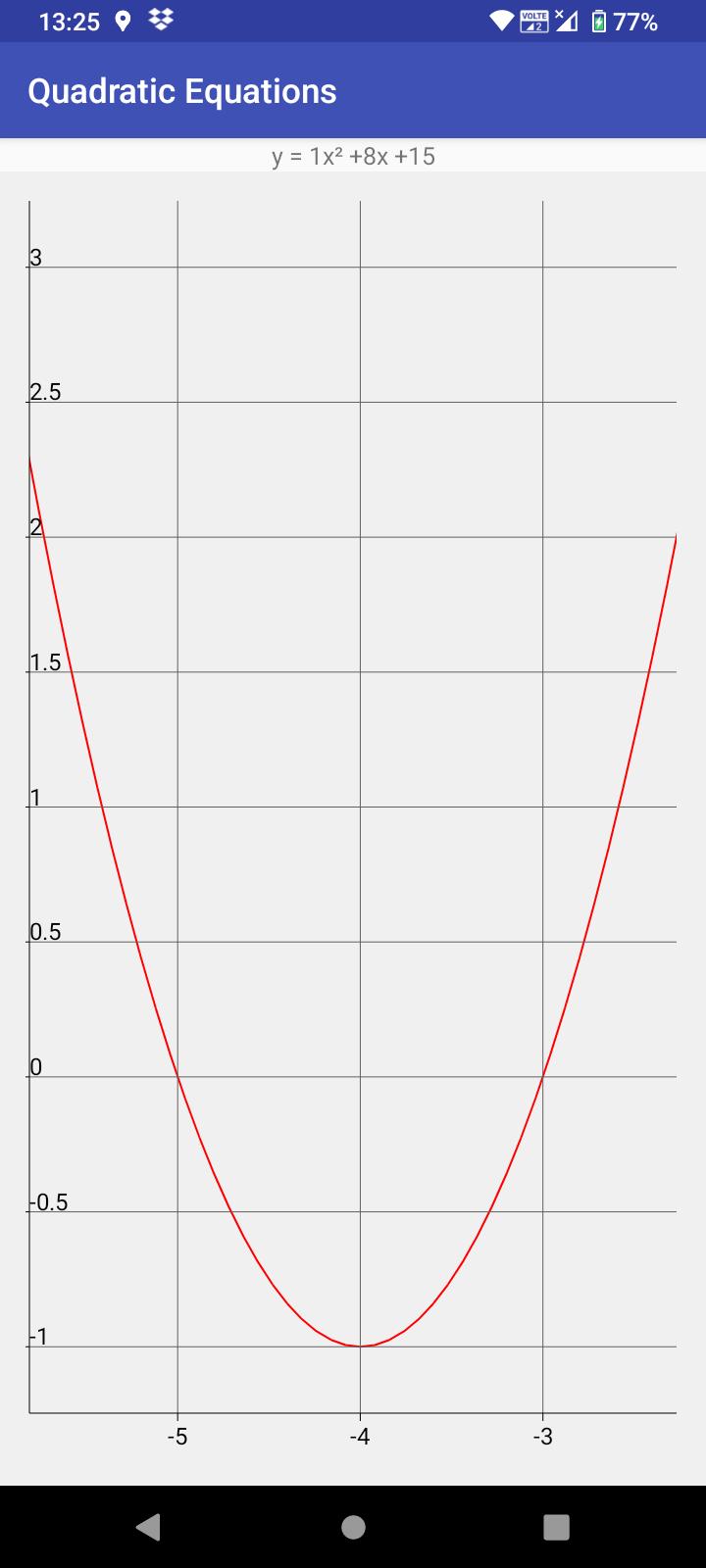
• Mostrar equação no gráfico

Observação :

1. Para aqueles que precisam de suporte, envie um e-mail para mim

NÃO utilize também a área de feedback para escrever perguntas, pois não é apropriado e não é garantido que consiga lê-las.

Uma equação quadrática é uma equação de segundo grau, o que significa que contém um termo com o quadrado de uma variável. A forma geral de uma equação quadrática é:

```

machado² + bx + c = 0

```

onde a, b e c são constantes e a ≠ 0.

Resolvendo Equações Quadráticas

Existem vários métodos para resolver equações quadráticas, incluindo:

1. Fatoração:

Se a equação quadrática puder ser fatorada em dois fatores lineares, ela poderá ser resolvida definindo cada fator igual a zero e resolvendo a variável. Por exemplo, se:

```

x² - 5x + 6 = 0

```

pode ser fatorado como:

```

(x - 2) (x - 3) = 0

```

então as soluções são x = 2 e x = 3.

2. Completando o Quadrado:

Este método envolve adicionar e subtrair uma constante à equação quadrática para criar um trinômio quadrado perfeito. A raiz quadrada do quadrado perfeito pode então ser calculada para resolver a variável.

3. Fórmula quadrática:

A fórmula quadrática é uma fórmula geral que pode ser usada para resolver qualquer equação quadrática:

```

x = (-b ± √(b² - 4ac)) / 2a

```

onde a, b e c são os coeficientes da equação quadrática.

Natureza das Raízes

O discriminante de uma equação quadrática, que é b² - 4ac, determina a natureza das raízes:

* Discriminante positivo: Duas raízes reais distintas

* Discriminante zero: Uma raiz real (uma raiz dupla)

* Discriminante negativo: Sem raízes reais (duas raízes complexas)

Aplicações de equações quadráticas

As equações quadráticas têm inúmeras aplicações em vários campos, incluindo:

* Movimento de projéteis

* Análise de circuito

* Problemas de otimização

* Modelagem de curvas parabólicas

* Resolvendo problemas geométricos

Encontre raízes, máximo ou mínimo da equação quadrática

Este aplicativo serve para calcular equações quadráticas.

Características

• Resolver equação quadrática

• Mostrar raízes reais e raízes complexas

• Calcular ponto máximo ou mínimo

• Salvar resultado em arquivo de texto

• Suporte em inglês, alemão, francês, italiano, espanhol, português, japonês, chinês tradicional e chinês simplificado

Recursos apenas na versão PRO:

• Sem anúncios

• Mostrar equação no gráfico

Observação :

1. Para aqueles que precisam de suporte, envie um e-mail para mim

NÃO utilize também a área de feedback para escrever perguntas, pois não é apropriado e não é garantido que consiga lê-las.

Uma equação quadrática é uma equação de segundo grau, o que significa que contém um termo com o quadrado de uma variável. A forma geral de uma equação quadrática é:

```

machado² + bx + c = 0

```

onde a, b e c são constantes e a ≠ 0.

Resolvendo Equações Quadráticas

Existem vários métodos para resolver equações quadráticas, incluindo:

1. Fatoração:

Se a equação quadrática puder ser fatorada em dois fatores lineares, ela poderá ser resolvida definindo cada fator igual a zero e resolvendo a variável. Por exemplo, se:

```

x² - 5x + 6 = 0

```

pode ser fatorado como:

```

(x - 2) (x - 3) = 0

```

então as soluções são x = 2 e x = 3.

2. Completando o Quadrado:

Este método envolve adicionar e subtrair uma constante à equação quadrática para criar um trinômio quadrado perfeito. A raiz quadrada do quadrado perfeito pode então ser calculada para resolver a variável.

3. Fórmula quadrática:

A fórmula quadrática é uma fórmula geral que pode ser usada para resolver qualquer equação quadrática:

```

x = (-b ± √(b² - 4ac)) / 2a

```

onde a, b e c são os coeficientes da equação quadrática.

Natureza das Raízes

O discriminante de uma equação quadrática, que é b² - 4ac, determina a natureza das raízes:

* Discriminante positivo: Duas raízes reais distintas

* Discriminante zero: Uma raiz real (uma raiz dupla)

* Discriminante negativo: Sem raízes reais (duas raízes complexas)

Aplicações de equações quadráticas

As equações quadráticas têm inúmeras aplicações em vários campos, incluindo:

* Movimento de projéteis

* Análise de circuito

* Problemas de otimização

* Modelagem de curvas parabólicas

* Resolvendo problemas geométricos